Subscribe to our newsletter
Noether’s Theorem: Symmetry Runs the Game #InternationalWomensDay
 Image: Pop Art Posters Celebrate Pioneering Women Scientists. Modified from (13)
Image: Pop Art Posters Celebrate Pioneering Women Scientists. Modified from (13)
How the creative genius of an unknown female mathematician unified two pillars of modern physics and laid the foundation for a new way of looking at the universe.
Symmetries are satisfying. A face which is equal on both sides in an advert for good genes – in everything from humans to swallows (2). It turns out that in addition to helping us find the perfect partner, symmetry is pulling the strings of the world we live in. For each particle of matter that exists, there is a corresponding anti-particle. Symmetry. The distribution of stars in the night sky is the same in whichever direction we look (3). Symmetry. Could this just be a coincidence? Do we put emphasis on these symmetric aspects of nature because we find them so pleasing… or is it something else?
Many symmetries occur in physics and these have many implications, however, we will consider a concept that links these symmetries to another landmark of physical law: conserved quantities. This link, established by German mathematician Emmy Noether, provides an explanation to things we take for granted. Everyday explanations, such as why we can ride bikes, and ideas that we are led to believe are fundamental truths, such as why energy is conserved, can be explained by Noether’s Theorem.
Who–ther’s Theorem?
Issues to do with energy conservation arose from Einstein’s theory of general relativity and many people viewed them as problems with the theory. The mathematician Hilbert described this as the ‘failure’ of the theory. Meanwhile, a German mathematician, Emmy Noether was making a lot of progress in analysing invariance problems – mathematical puzzles where quantities remain constant when changes are made to a system. Noether was beginning to understand these concepts whilst developing the necessary mathematical framework required to solve associated problems. In 1915, she was asked to use her insight and help resolve the problems with energy conservation in general relativity. Using her knowledge of invariance, Noether was able to clear up the problem and in a 1918 paper she stated and proved what is now known as ‘Noether’s Theorem’ (5). The theorem states,
“If a system has a continuous symmetry property, then there are corresponding quantities whose values are conserved in time.”(6)
Here, a ‘symmetry’ refers to some transformation performed on a physical system that would not affect measured quantities. The theorem states that the inverse is also true and so any observed conserved quantities explicitly require that there be a symmetry present within the system(6).
What does the theorem mean?
Noether’s theorem can be easily applied to everyday classical phenomena, such as a game of pool. If two pool balls were to collide on a table, they would collide in exactly the same way regardless of where they collided on the table, since the laws of physics are the same across the whole table. This would be a symmetry in space and corresponds to a conservation of momentum within the system (6). The outcome of this experiment would have been the same if this game of pool was played later that evening, another day that week, or at any other time. This is a symmetry in time and corresponds to a conservation in energy. In addition to these applications of Noether’s theorem in simple contexts, this relationship holds for all of physics: from space travel to Quantum Mechanics (7) and so is a very far-reaching theorem.
The symmetry that Noether described looks at symmetries of the Lagrangian. This quantity, the Lagrangian, is the difference between the energy associated with the movement of a particle and the energy associated with any interactions.
Lagrangian = Potential Energy – Kinetic Energy
At first glance, this may seem like a random quantity that has little physical meaning, but in fact, nature uses this quantity to determine the motion of particles.
Nature is efficient. In optics, light follows the path that takes the least time (Fermat’s principle) and more generally, the true path taken by a particle is such that it minimises a specific physical property of the path (3). This property is called the Action and is defined as the time integral over the path of the Lagrangian of the system(8).
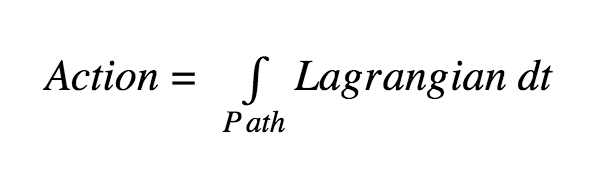 It can be shown that this minimisation principle allows us to identify the link between symmetries and conservation laws (7). Since the real path is at a minimum of the action, a stationary point, small modifications can be made that to a first approximation do not affect the action of the path. By invoking a symmetry of the system, we can cancel parts of the original path with parts of the modified path. This results in an equality that shows there is a quantity that is the same before and after the motion of the particle: a conservation law (7).
It can be shown that this minimisation principle allows us to identify the link between symmetries and conservation laws (7). Since the real path is at a minimum of the action, a stationary point, small modifications can be made that to a first approximation do not affect the action of the path. By invoking a symmetry of the system, we can cancel parts of the original path with parts of the modified path. This results in an equality that shows there is a quantity that is the same before and after the motion of the particle: a conservation law (7).

Why is this important?
One must not confuse Noether’s lack of widespread popularity with the idea that Noether’s work was insignificant. Noether’s theorem underpins many common ideas within physics, a commonly known example being the conservation of charge. The invariance of a quantum wavefunction when undergoing a phase shift gives rise to conservation of charge and, ultimately, Maxwell’s equations (3). Newton’s first law describes the conservation of momentum, however, Noether’s theorem is even more fundamental and says that this comes from the symmetry of universe, since the laws of physics are the same at all points in space.
When Noether first published her theorem, she managed to approach these invariant, conserved quantities from a very general viewpoint, which amazed her contemporaries (including Einstein) (5). Since Noether also proved this statement’s inverse (if we observe a conserved quantity in a particular system, there must be a corresponding symmetry) hypotheses could be tested by observation of (or lack of) conservations within physical systems. Noether also showed that these relationships hold for infinite numbers of dimensions and showed that the theorem holds for a variety of other technical situations, which describe more specific versions of the symmetries, further generalising this relationship (5).
The work of Noether is often referred to as the ‘starting point’ of Gauge Theory (9). Similarly, to Noether’s theorem, Gauge Theory explores the effects of looking at changing the coordinate systems of a physical system, by making local transformations (see Gauging the Importance of Symmetries) (10). This may initially appear to be very abstract, but Gauge Theories are used to describe the interaction of matter (and light) at the most fundamental level.
What makes Noether’s theorem so phenomenal, is that it is the basis of almost all of the physical laws we previously thought were fundamental. That ‘Energy cannot be created or destroyed’, is not a law of nature but a consequence of a symmetry. This is one of many slogans of science that we assume to be rudimentary, when in fact we can trace their origins back even further to something much more fascinating. It is hard to comprehend how much information must be in each syllable when one sentence can describe an idea on which almost every interaction in the universe is built.
The Unsung Hero
Emmy Noether was a creative genius, with deep and fundamental insight that unified two of the foundations of physics; symmetries and conservation laws. This raises the question as to why Emmy Noether or her contribution to physics is not as familiar to us as the work of Einstein, Newton or Maxwell. A significant contributing factor is that Noether suffered to pursue mathematics as a career. She was a Jewish, pacifist, socialist woman living in Germany. She was only allowed to attend undergraduate lectures to ‘audit’ them and despite having amazed all academics whom she worked with Emmy Noether was not able to secure a permanent academic position – not to mention getting paid. With no salary, tenure or respect, Emmy Noether lived for mathematics (11). Although not formally recognized as a professor, her passion fueled her to find ways around the society in which she found herself and she was able to lecture as an assistant to David Hilbert (5).
However, in addition to facing so much adversity at the time, I believe that the achievements of Emmy Noether remain unsung due to the timing and nature of her brilliance. Emmy Noether identified concepts that were central to the work of titans in science, and thus was competing with well-established (male) scientists. Stating that something arises from Newton’s Third Law was more in keeping with 1900s Germany than describing how it arises from Noether’s theorem or a symmetry in space. In addition to prejudice due to her gender and beliefs, Noether was also competing with chronology.
In her obituary in the New York Times, Einstein described Noether as “the most significant creative mathematical genius thus far produced since the higher education of women began”, describing her work as being of “enormous importance in the development of the present-day younger generation of mathematicians”. (12)
Noether and her work provides a starting point for many of the theories we use to describe modern physics, but she has been forgotten underneath all those whom her work supports.
Gauging the Importance of Symmetries
Symmetries are identified as transformations that are performed on objects, with quantities being the same before and after the transformation: an invariant quantity. Many of the symmetries that one may think of when given this definition are Global Symmetries, which do not depend on spacetime. The same transformation is performed at any point in space and at any time, with the symmetric quantity being conserved for all of these transformations, e.g. multiplying a wavefunction by ei everywhere. When symmetries are continuous and depend on spacetime, they are Gauge Symmetries. These symmetries do not apply globally and so are often referred to as being local. The image below attempts to illustrate this difference pictorially between local and global transformations. In the global transformation, the entire sphere is rotated. In the local transformation, however, the rotation made at each point depends on the position of that point on the sphere (14).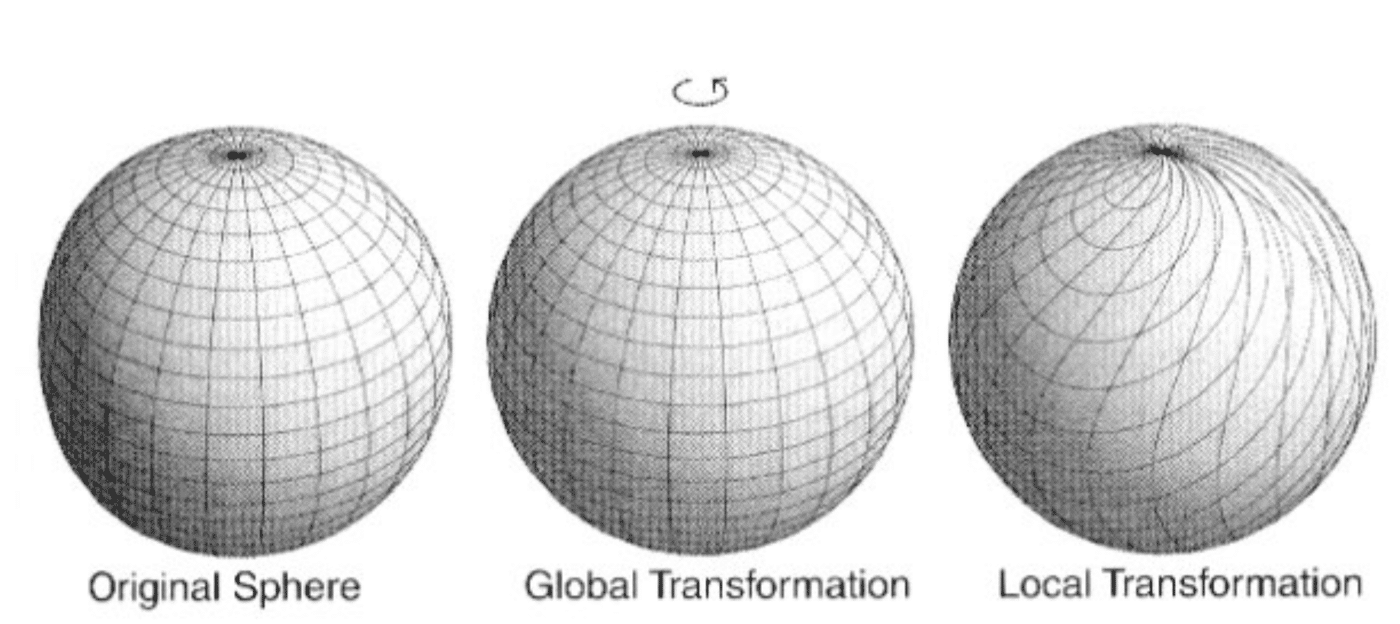
Image: Visual Interpretation of Local vs Global Transformations (14)
As an example, we can consider the description of the magnetic field, , as the curl of the magnetic vector potential, A, giving B=∇A (this comes from Maxwell’s Equation,∇B=0 ). We can identify changes that can be made to this magnetic vector potential, A, that will not affect the observed magnetic field. One could define a continuous scalar field, say f, and create a new potential,
A’ =A + ∇f,
that will produce an identical curl and therefore the exact same magnetic field as the original magnetic vector potential (15). Here we have seen an example of a transformation that varies depending on the position in spacetime and produces an invariant quantity. This is a gauge symmetry.
Gauge theories use these symmetries to simplify problems and are common across much of physics describing the basic interactions between the foundations of the universe. Quantum Electrodynamics which describes the interactions of light and matter is a gauge theory, as is the theory of Quantum Chromodynamics, which describes how quark and gluons (the particles that make up protons and neutrons) interact through the strong force. In fact, gauge theories are the bedrock of the standard model, the currently favoured description of all constituents of matter and their interactions. (16)
Author

References
(1) Image: Pixababy
(2) Knapton S. The science of sexiness: why some people are just more attractive. The Telegraph. April 2015.
(3) Goldberg D. Emmy Noether. The Universe in the Rearview Mirror. 1st Edition ed. Plume 2014; 2014. pp. 105.
(4) Carroll S. Cosmic Variance – Energy Is Not Conserved, Discover Magazine Blog. Available from: http://blogs.discovermagazine.com/cosmicvariance/2010/02/22/energy-is-not-conserved/#.WlM8V99l9nJ [Accessed December 2017].
(5) Teicher M. Emmy Noether: her heritage. Universitat Politècnica De Catalunya. Facultat De Matemàtiques; 2008.
(6) Thompson WJ. Angular momentum : an illustrated guide to rotational symmetries for physical systems. New York ; Chichester: Wiley-Interscience; 1994.
(7) Feynman RP(P, 1918-1988. The character of physical law. London: Penguin; 1992.
(8) Hand LN, 1933-. Analytical mechanics. Cambridge: Cambridge University Press; 1998.
(9) Hojman S. Symmetries of lagrangians and of their equations of motion. Journal of Physics A: Mathematical and General. 1984;17(12): 2399-2412.
(10) Quigg C. Gauge theories of the strong, weak, and electromagnetic interactions. 2nd ed. Princeton, NJ: Princeton University Press; 2013.
(11) Eschner K. Mathematician Emmy Noether Should Be Your Hero, Smithsonian
. Available from: https://www.smithsonianmag.com/smart-news/emmy-noether-should-be-your-hero-180962591/ [Accessed December 2017].
(12) Einstein A, 1879-1955.
Emmy Noether, Professor Einstein Writes in Appreciation of a Fellow-Mathematician.. New York Times. 5th May 1935.
(13) Jones J. Pop Art Posters Celebrate Pioneering Women Scientists… Posters of Marie Curie, Ada Lovelace & More. Available from: http://www.openculture.com/2017/11/pop-art-posters-celebrate-pioneering-women-scientists.html [Accessed December 2017].
(14) Universe Review. Gauge Theory and the Standard Model, Elementary Particles and the World of Planck Scale. Available from: http://universe-review.ca/I15-04-gauge2.jpg [Accessed January 2018].
(15) Errede S. THE MAGNETIC VECTOR POTENTIAL, Lecture Notes 16. UIUC Physics 435 EM Fields & Sources I, Fall Semester.; 2007.
(16) Hughes C. A brief discussion on Gauge Theories. Cambridge University; 2015.
(17) Quantum wonders: The field that isn’t there. Seven wonders of the quantum world Magazine Issue 2759 ed. New Scientist; 2010.
(18) Angier N. The Mighty Mathematician You’ve Never Heard Of. The New York Times. March 2012: pp. D4.
(19) Brizard AJ, author. An introduction to Lagrangian mechanics. 2nd ed. New Jersey ; London: World Scientific Publishing Co Pte. Ltd; 2015.
(20) Feynman RP, Leighton RB, Sands M, Treiman SB. The Feynman Lectures on Physics. Physics Today. 1964;17(8): 45-46.
(21) Kosmann-Schwarzbach Y. The Noether theorems: invariance and conservation laws in the twentieth century. 1st Edition. ed.; 2010.
(22) Prof. Andrew O. Parry. Conversation with Prof. A. O. Parry. 2017.



